Tap for more steps Set the x − 1 x 1 equal to 0 0 x − 1 = 0 x 1 = 0 Add 1 1 to both sides of the equation x = 1 x = 1 x = 1 x = 1 The equation is undefined where the denominator equals 0 0, the argument of a square root is less than 0 0, or the argument of aDecreasing on (100) Of®) is decreasing on (0,5);F0(x) DNE when x= 7 For problems 715, calculate each of the following (a) The intervals on which f(x) is increasing (b) The intervals on which f(x) is decreasing (c) The intervals on which f(x) is concave up (d) The intervals on which f(x) is concave down (e) All points of in ection Express each as an ordered

Determine The Values Of X For Which F X X 2 X 1 X 1 Is Increasing Or Decreasing
How to tell if f(x) is increasing or decreasing
How to tell if f(x) is increasing or decreasing- = – e x(1 – x) (x – 1)(2x 1) f is increasing when f'(x) ≥ 0 and decreasing when f'(x) ≤ 0 Thus f is increasing in –1/2, 1Select one Of(x) is decreasing on (0,1);




Rd Sharma Class 12 Solutions Chapter 17 Increasing And Decreasing Functions
CBSE CBSE (Arts) Class 12 Question Papers 17 Textbook Solutions Important Solutions 24 Question Bank Solutions Concept Increasing and Decreasing Functions video tutorial ;The first thing to note is that the zeros of the derivative occur at x=1, x=2, and x=3 So, you must select a number on each of the intervals (inf,1), (1,2), (2,3), and (3,inf) to determine if the derivative is positive or negative on that interv 2nd PUC Maths Application of Derivatives NCERT Text Book Questions and Answers Ex 62 Question 1 Find the intervals in which the function f given by f (x) = 3x 17 is strictly increasing in R Answer f (x) = 3x 17 f' (x) = 3 > 0 , ∀ x ∈ R hence f (x) is strictly increasing
1) If f0(x) > 0 for all x in I, then f is increasing(%) on I 2) If f0(x) < 0 for all x in I, then f is decreasing(&) on I Proof We have proved the flrst result as a corollary of Mean Value Theorem in class Here to remind ourselves MVT we will prove the second one Let f0(x) < 0 on the interval I Pick any two points x1 and x2 in I where x1Test whether the function is increasing or decreasing f(x) = x1x, x ∈ R, x ≠ 0, Maharashtra State Board HSC Science (Computer Science) 12th Board Exam Question Papers 181 Textbook Solutions Online Tests 60 Important Solutions 3532 Question Bank SolutionsIncreasing on (1c0) OfQ) is increasing on (01);
If f(x) > 0, then the function is increasing in that particular interval If f(x) < 0, then the function is decreasing in that particular interval Example 1 Find the intervals in which f(x) = 2x³x²x is increasing or decreasing Solution f(x) = 2x 3 x 2 x Step 1 f'(x) = 6x² 2x ÷ by 2 ⇒ 3x²x10 Step 2 f'(x) = 0Answer Find the intervals on which f ( x) is increasing, the intervals on which f ( x) is decreasing, and the local extrema f ( x) = x ln x − x Calculus for Business, Economics, Life Sciences, and Social Sciences 13th Chapter 4 Graphing and Optimization Section 1 First Derivative and GraphsQuestion 1 Find The Intervals On Which F(x) Is Increasing, Decreasing And Its Local Extrema F(x) = X 3x 2 2 Summarize The Pertinent Information Obtained By Applying Graphing Strategy And Sketch The Graph Of F(x) = 2x X3 3 Use L'Hopital Rule To Find (@2x 1) Xto



Finding The Values Of X When F X Is Increasing Decreasing The Student Room




Increasing Decreasing Functions A Function F Is Increasing On An Interval If For Any X 1 And X 2 In The Interval X 1 X 2 Implies F X 1 F X Ppt Download
Functions are increasing, decreasing and constant when you plot the graph of the function in a coordinate system Let's define the meaning of these functions Increasing function A function is increasing in an interval for any and if implies Example Let be a function Find all the values for the function to plot the graph xSo, f (x) is increasing on (−∞, 2−1 ∪21 ,∞) (b) For decreasing function, ⇒ x24x2 −1 ≤ 0 `f'(x)=(1x^2)/(x^21)^2` If the resulting value of f'(x) is negative, the function is decreasing in that interval If it is positive, the function is increasing




Find The Intervals In Which F X 4x 2 1 X Is Increasing Or Decreasing



Increasing Decreasing Functions Examples
This video screencast was created with Doceri on an iPad Doceri is free in the iTunes app store Learn more at http//wwwdocericom On the other hand, if by "itexf/itex is strictly increasing at itexx/itex" you mean "there is an open neighbourhood of itexx/itex on which itexf/itex is strictly increasing" then itexf/itex is not strictly increasing or decreasing at 0 1 If itexX/itex consists of a single point then tex(\forall x \in X)(\forall yIncreasing on (500) None of these The graph of the dermative of a
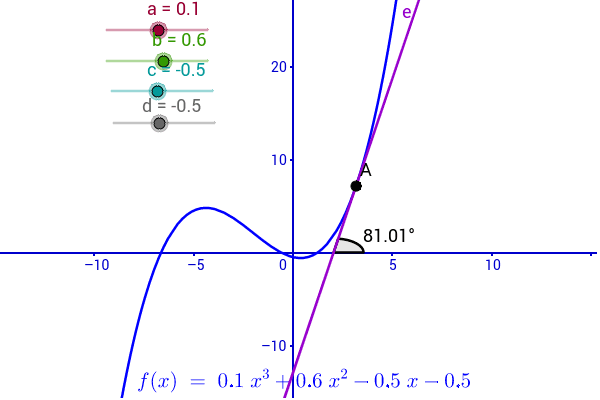



Increasing And Decreasing Function Geogebra




Classxii Sub Mathematics Topic Increasing Decreasing Increasing Decreasing
∴ f'(x) > 0 f(x) is increasing on (0, 1) Since 0 < x < 157 099 < x99 < (157)99 0 × 100 < 100x99 < (157)99 × 100 0 < 100x99 < (157)99 × 100 Since 0 < x < 𝜋/2 So x is in 1st quadrant ∴ cos x is positive Thus, f(x) is strictly decreasing for none of the intervals So, (D) is the correct answer Show More Find f'(x) f'(x) = 4 cos (x) sin (x) Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice OA The function is increasing on the open interval(s) ,0U „ and decreasing on the open interval(s) (Simplify your answersA) 2 < 0 for t > 0, so g ( t) < 1 for t > 0 Using simple algebra it is possible to prove that g ( x) = f ( 1 / x) = a x − 1 x is strictly increasing for x > 0, a > 0, a ≠ 1 and x being rational The extension to irrational values of x is easily done by considering sequences of rationals converging to x




Answered 3 3 Increasing And Decreasing Functions Bartleby
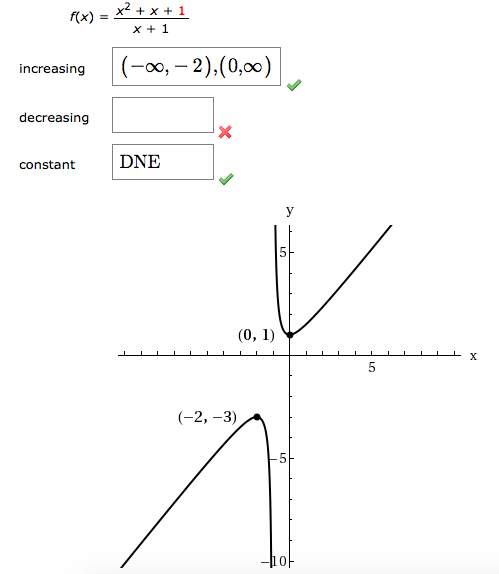



Determine The Intervals On Which The Function Is Chegg Com
If f'(x) = (x 1)e, which of the following statements is true about the function J?The function is decreasing over its domain (Note that the function is not defined at x = 0, since division by zero is undefined) That the function increases is apparent from a visual inspection of the graph But one might ask, "Why?" Let's rewrTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find the intervals in which `f(x)=(x1)^3(x2)^2`is increasing or decreasing




Ex 6 2 6 Find Intervals In Which Functions Strictly Increasing




Determine The Values Of X For Which F X X 2 X 1 X 1 Is Increasing Or Decreasing
If f′(x) > 0, then f is increasing on the interval, and if f′(x) < 0, then f is decreasing on the interval This and other information may be used to show a reasonably accurate sketch of the graph of the function Example 1 For f(x) = x 4 − 8 x 2 determine all intervals where f is increasing or decreasing 1 determine the interval(s) where the function f(x)= 1 / 2x10 is a) positive b) Increasing 2 Consider the function f(x) = 3 / 4x5 a) Determine the key features of the function i) Domain and range ii)Intercepts iii) EquationsThus, at the transition (from left to right) through the point \(x = 1\), the function changes from increasing to decreasing, ie \(x = 1\) is the maximum point of the function Similarly, \(x = 3\) is the minimum point of the function Figure 24 Figure 25




Show That F X 1 1 X 2 Is Neither Increasing Nor Decreasing On R
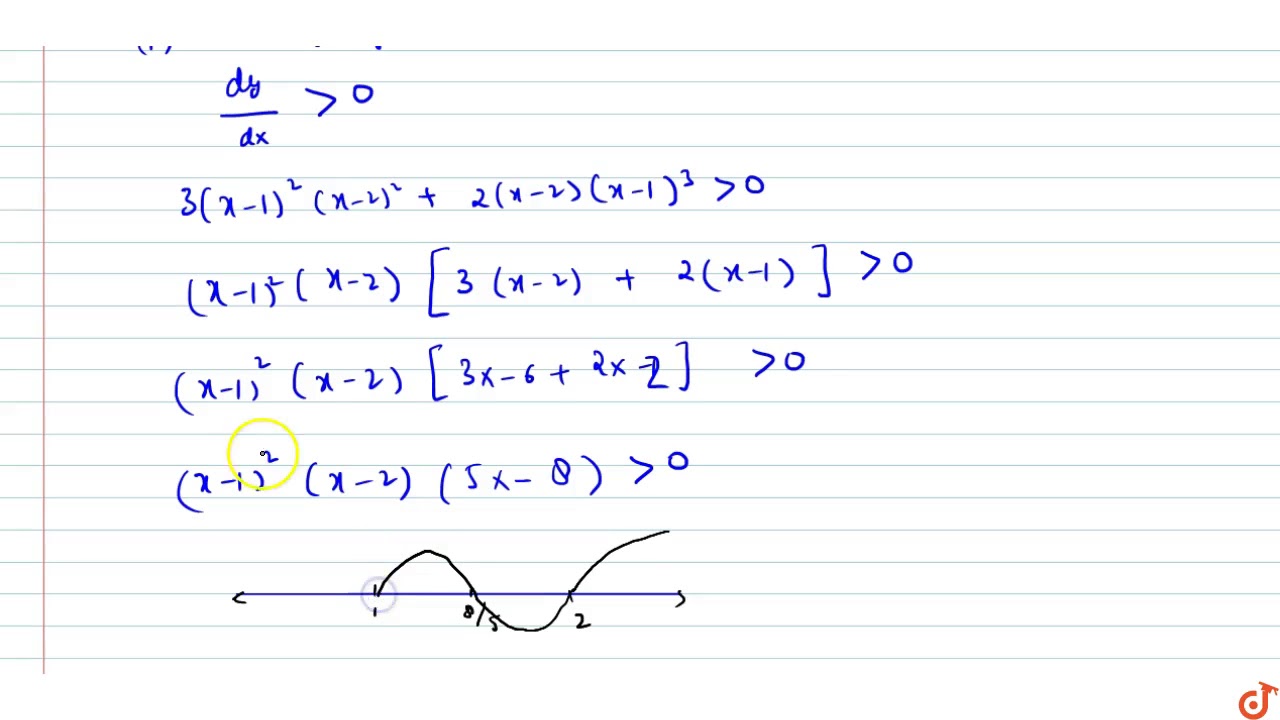



Find The Intervals In Which F X X 1 3 X 2 2 Is Increasing Or Decreasing Youtube
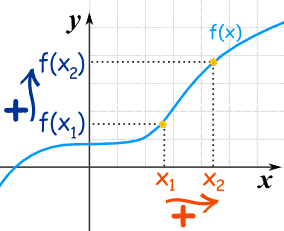
1 This proof is from theorem 140 from Hardy's Inequalities Let f(x) = ln(1 1 x)x = x(ln(x 1) − ln(x)) We refer to the mean value theorem for each differentiable g , g(x h) − g(x) = hg ′ (x θh) for θ ∈ (0, 1) Applying the MVT to g(x) = ln(x), we get ln(x 1) − ln(x) = 1 x θX Definitions of Increasing and Decreasing Functions A function is increasing on an interval when, for any two numbers and in the interval, implies A function is decreasing on an interval when, for any two numbers and in the interval, implies x 1 < x 2 f x 1 > f x 2 f x 1 x 2 x 1 < x 2 f x 1 < f x 2 f x 1 x 2 THEOREM 35 Test for IncreasingF(x) is an odd function Again f ( x ) = ( e 2 x − 1 e 2 x 1 ) ⇒ f ′ ( x ) = 4 e 2 x ( 1 e 2 x ) 2 > 0 ∀ n ∈ R ⇒ f ( x ) is an increasing function
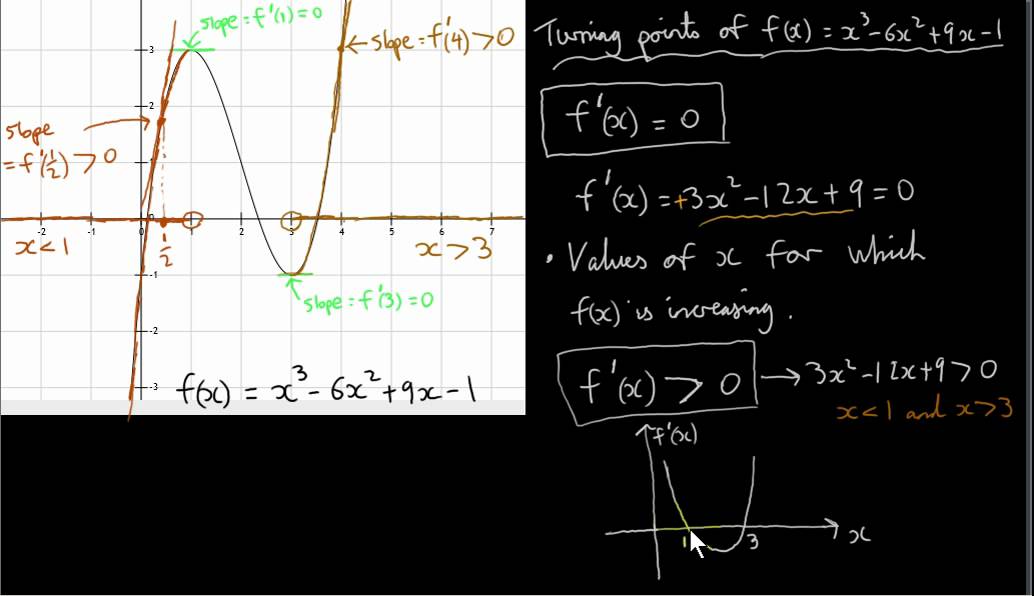



How To Find The Values Of X For Increasing And Decreasing F X Youtube




Find The Intervals In Which The Function F X Log 1 X Frac 2 X 2 X Is Strictly Increasing Or Decreasing
determine the intervals over which the function is increasing, decreasing, or constant f(x)=√x^21 Calculus Consider the function f(x)=ln(x)/x^6 For this function there are two important intervals (A,B and B,∞) where A and B are critical numbers or numbers where the function is undefinedSolution for If ø(x) =(x) f(1x) and f"(x) Misc 7 Find the intervals in which the function f given by f (x) = x3 1/𝑥^3 , 𝑥 ≠ 0 is (i) increasing (ii) decreasingf(𝑥) = 𝑥3 1/𝑥3Finding f'(𝒙) f'(𝑥) = 𝑑/𝑑𝑥 (𝑥^3𝑥^(−3) )^ = 3𝑥2 (−3)^(−3 − 1)= 3𝑥2 – 3𝑥^(−4)= 3𝑥^2−3/𝑥^4 = 3(𝑥^2−1/𝑥^4 )Putting f'(𝒙) = 03(𝑥^2− (टीचू) Maths



Q Tbn And9gcqfhuxhmizntsns V1x7khz5m A5m8vqbqk2v3lmpebzl 5tjrm Usqp Cau




View Question Properties Of This Reciprocal Function F X X 1 X 1
1Answer 1vote answeredby ShrutiBharti(345kpoints) selectedby Vikash Kumar Best answer Given, f(x) = (x 1)3 (x 2)2 On differentiating both sides wrt x, we get Now, we find intervals and check in which interval f(x) is strictly increasing and strictly decreasingFind the intervals where f is increasing and decreasing if f(x) = (1/5)x^5 Analyzing Functions In order to analyze where does a function is increasing, decreasing, or constant, we have to graphPopular Problems Calculus Find Where Increasing/Decreasing f (x)=x1/x f (x) = x 1 x f ( x) = x 1 x Find the derivative Tap for more steps Differentiate Tap for more steps By the Sum Rule, the derivative of x 1 x x 1 x with respect to x x is d d x x d d x 1 x d d x x d d x 1 x



Increasing And Decreasing Functions



Classxii Sub Mathematics Topic Increasing Decreasing Increasing Decreasing
Increasing on (1,co) OO) is decreasing on (601);Show that F(X) = E1/X, X ≠ 0 is a Decreasing Function for All X ≠ 0 ?Section 51 The First Derivative Increasing/Decreasing Test (a) If f0(x) > 0onaninterval,thenf is increasing on that interval (b) If f0(x) < 0onaninterval,thenf is decreasing on that interval Definition A critical number of a function f is a number c in the domain of f such that either f0(c)=0orf0(c)doesnotexist 1 Find the critical numbers for f(x)=x2 6x




Determine For What Values Of X The Function F X X 3 1 X 3 X 0 Is Strictly Increasing Or Strictly Decreasing




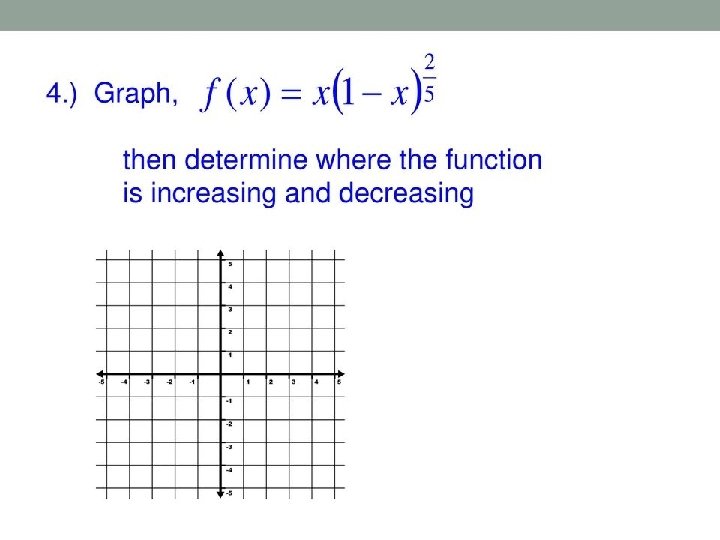
Misc 7 Find Intervals F X X3 1 X3 X 0 Is Increasing
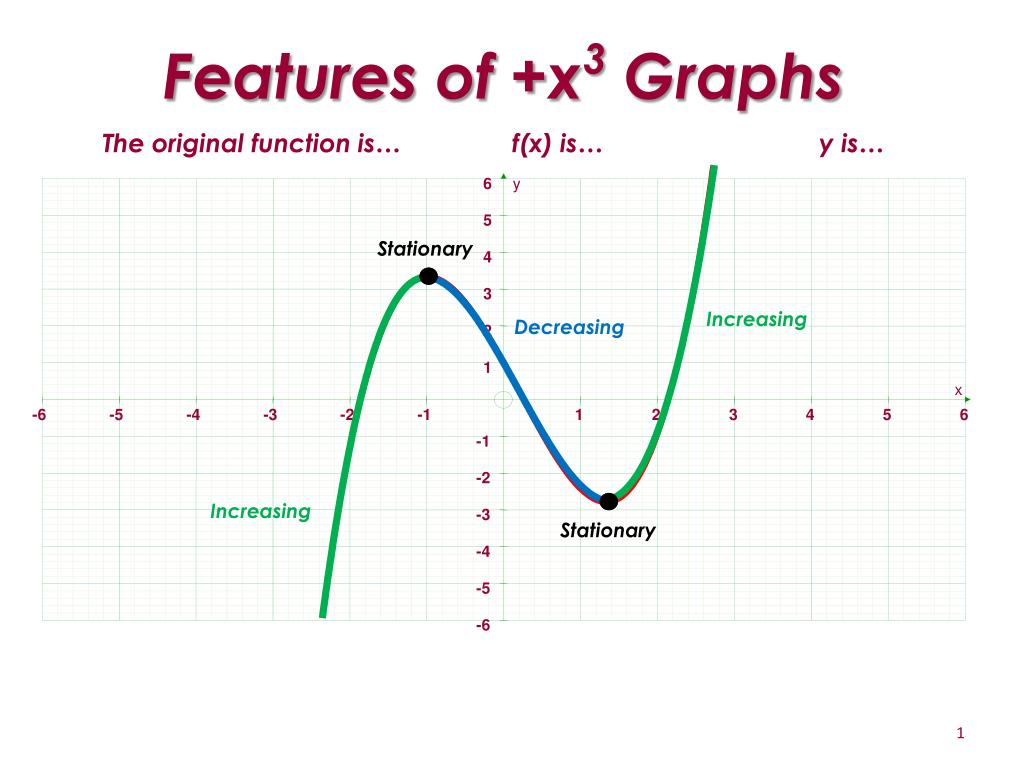
Figure 335 Number line for f in Example 332 In summary, f is increasing on the set ( − ∞, − 1) ∪ (3, ∞) and is decreasing on the set ( − 1, 1) ∪ (1, 3) Since at x = − 1, the sign of f'\ switched from positive to negative, Theorem 332 states that f( − 1) is a relative maximum of fThe total cost C(x) in Rupees associated with the production of x units of an item is given by C(x) = 0007 x – 0003 x 2 15 x 4000 Find the marginal cost when 17 units are produced HereFind the intervals in which the function f (x) = 4 x 4 − x 3 − 5 x 2 2 4 x 1 2 is (a) strictly increasing, (b) strictly decreasing Medium View solution




Increasing And Decreasing Function 1 Strictly Increasing Function




Graphs Of Functions Text Example Solutionthe Graph Of F X X Is By Definition The Graph Of Y X We Begin By Setting Up A Partial Table Ppt Download
Hence, f′(x) >0 f ′ ( x) > 0 in the interval (−∞,0) ( − ∞, 0) so, the function is increasing in the interval (−∞,0) ( − ∞, 0) Substitute x = 1 x = 1 in the firstorder Strictly speaking it is neither f(1)=0 is a constant However, f'(x) = 2(x2)(x1)(x2)^2, so f'(1)=1 Note that f' is continuous near 1 So, f'(x) is positive near 1 and f(x) is increasing near 1 Note For a number a, the phrase "near a" means "in some open interval containing a" Get an answer for '`f(x) = (x^2 2x 1)/(x 1)` Find the critical numbers, open intervals on which the function is increasing or decreasing, apply first derivative test to



How To Find Increasing Intervals By Graphing Functions Calculus 1




How To Find Increasing And Decreasing Interval For Continuous Rational Function Youtube
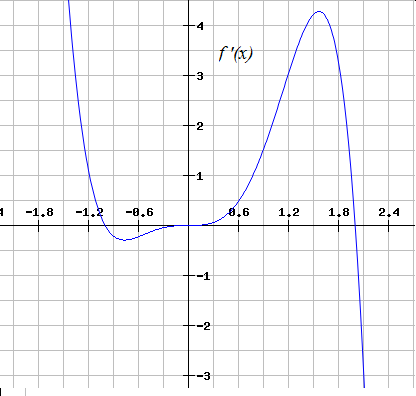
The derivative is positive outside of 2,1 and is negative inside of 2,1We can conclude that f is increasing outside of 2,1 and decreasing inside of 2,1The graph is shown below We saw that the values of x such that the derivative is 0 was of special interestF0(x) = 0 when x= 1 and x= 5;




Find The Intervals In Which F X 2log X 2 X 2 4x 1 Is Increasing Or Decreasing Maths Application Of Derivatives Meritnation Com




Find The Interval On Which The Following Function Is A Strictly Increasing B Strictly Decreasing F X 3x 4 4x 3 12x 2 5




Ex 6 2 11 Prove F X X2 X 1 Is Neither Strictly Increasing



Determine For What Values Of X The Function F X X 3 1 X 3 X 0 Is Strictly Increasing Or Strictly Decreasing Sarthaks Econnect Largest Online Education Community



Q Tbn And9gcsmm4ktmxrxm10kmsg3wqo5rzire Ogwbm0v2tajixhbesgniod Usqp Cau



Ppt Increasing Powerpoint Presentation Free Download Id
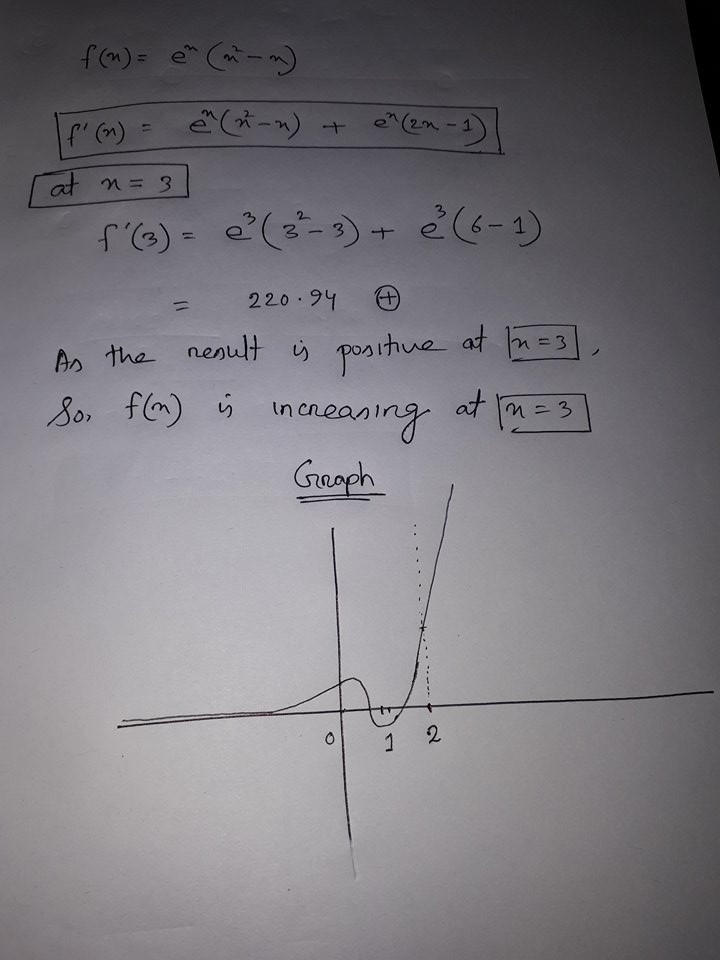



Is F X E X X 2 X Increasing Or Decreasing At X 3 Socratic




Calc 1 Pod 43 Find The Intervals On Which F Is Increasing And Decreasing F X X 2 Ln X 2 2 Youtube



Increasing And Decreasing Functions



Use A Graph To Determine Where A Function Is Increasing Decreasing Or Constant College Algebra




Intervals In Which Function Is Increasing Or Decreasing Problem Example 1 Youtube




Intervals On Which A Function Is Increasing Chegg Com




Is The Function F X Increasing Or Decreasing Over The Interval 2 Lt X Lt 1 Brainly Com



Http Www Mast Queensu Ca Math121 Assignments Unit06 Pdf




Determine The Values Of X For Which F X X 2 X 1 X 1 Is Increasing Or Decreasing




Find The Intervals In Which F X X 1 X 3 Is 1 Strictly Increasing 2 Strictly Decreasing Brainly In
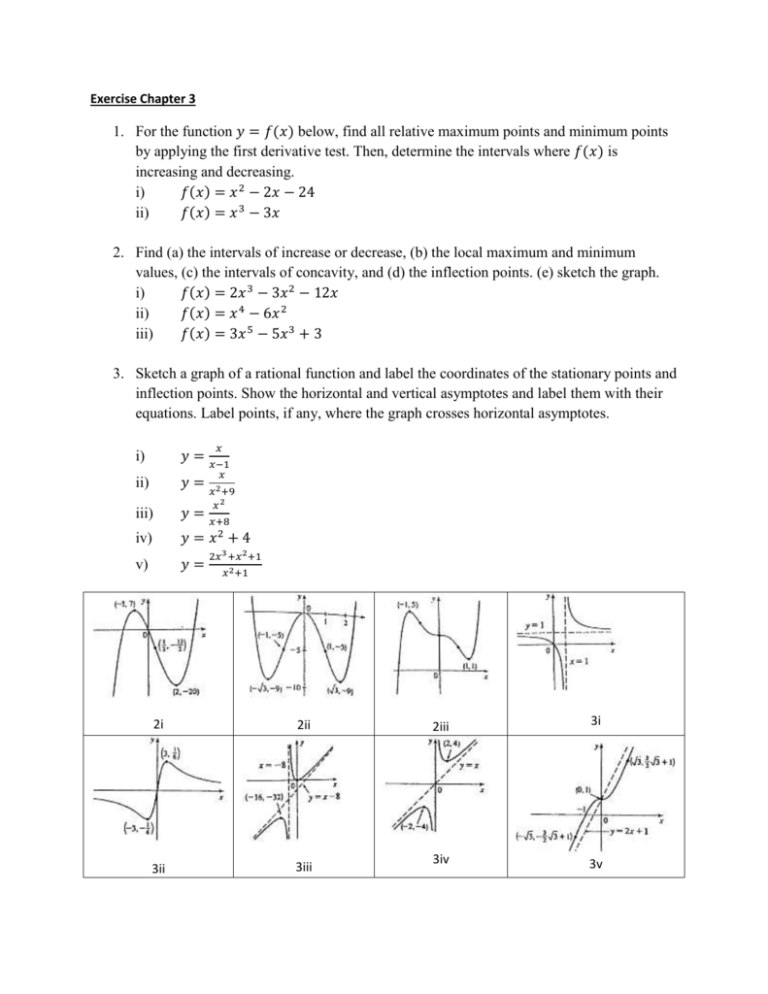



Exercise Chapter 3 Mathcfs Students Page




Misc 7 Find Intervals F X X3 1 X3 X 0 Is Increasing




X 1x Is Increasing On 1



Find The Intervals In Which The Function F X Log 1 X X 1 X Is Strictly Increasing Sarthaks Econnect Largest Online Education Community
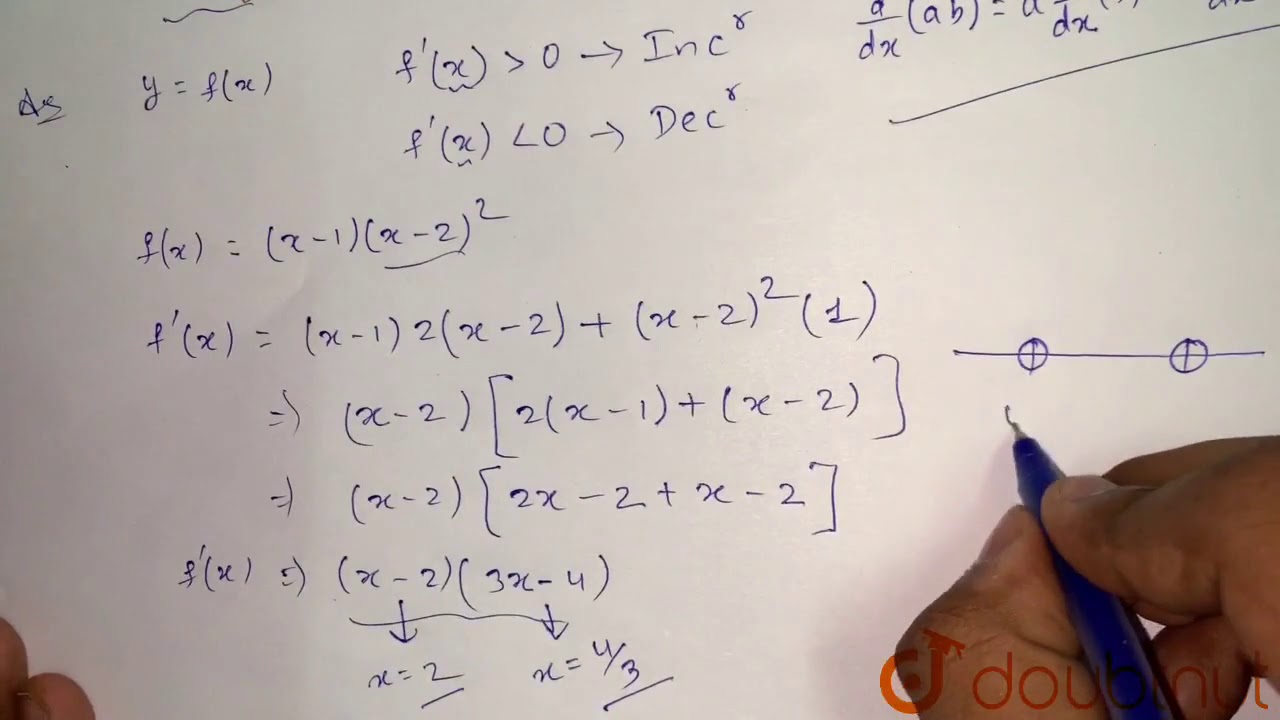



Find The Intervals In Which F X X 1 X 2 2 Is Increasing Or Decreasing Youtube
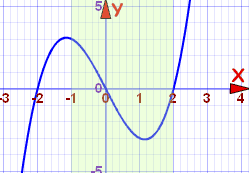



Increasing And Decreasing Functions
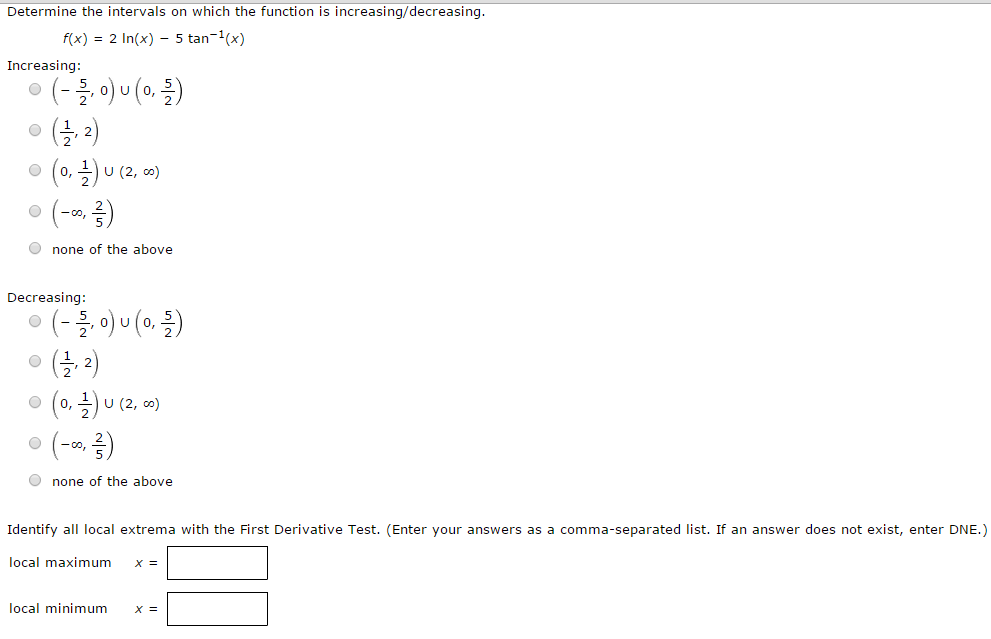



Determine The Intervals On Which The Function Is Chegg Com



Http Www Math Tamu Edu Mayaj Chapter5 Sec5p1completed Pdf



Joerg Endrullis




Rd Sharma Class 12 Solutions Chapter 17 Increasing And Decreasing Functions




5 3 A Curve Sketching Ppt Video Online Download
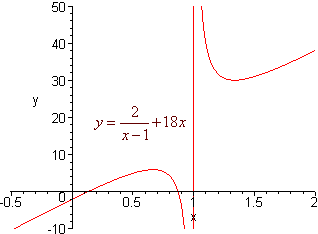



Increasing And Decreasing Functions




The Graph Of The Function F X X 4 X 1 Is Shown Below Which Statement About The Function Is Brainly Com




Ex 6 2 19 Mcq The Interval In Which Y X2 E X Is Increasing




Show That F X 1 X Is A Decreasing Function On 0 Oo
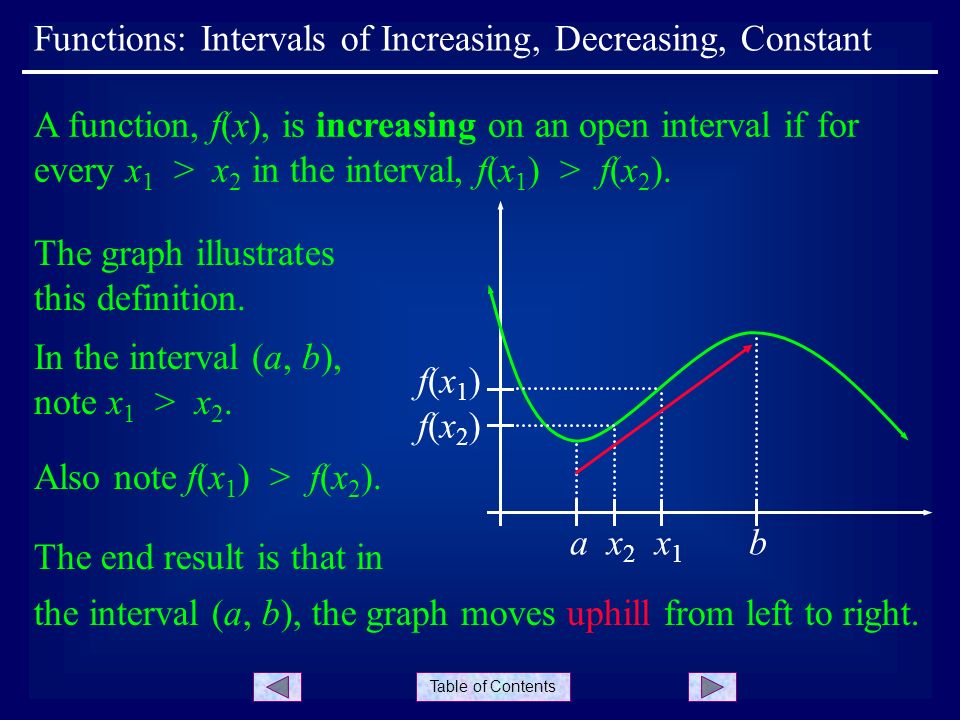



Table Of Contents Functions Intervals Of Increasing Decreasing Constant A Function F X Is Increasing On An Open Interval If For Every X 1 X 2 In Ppt Download
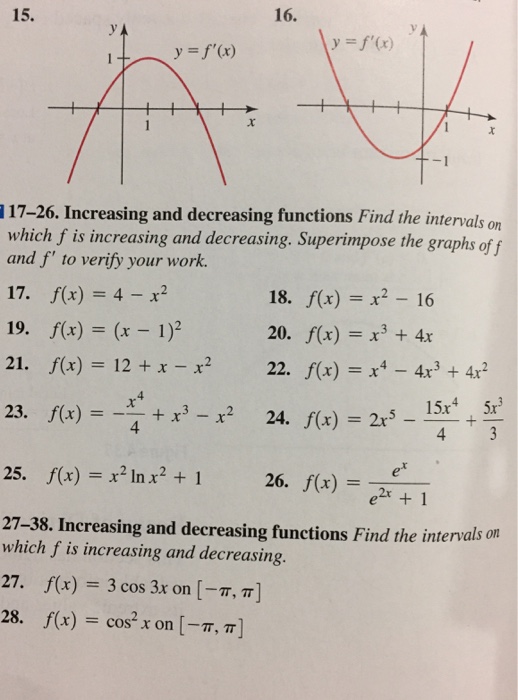



Increasing And Decreasing Functions Find The Chegg Com



Increasing And Decreasing Functions




Prove That The Function F Given By F X X2 X 1 Is Neither Strictly Increasing Nor Strictly Decreasing On 1 1 Mathematics Shaalaa Com
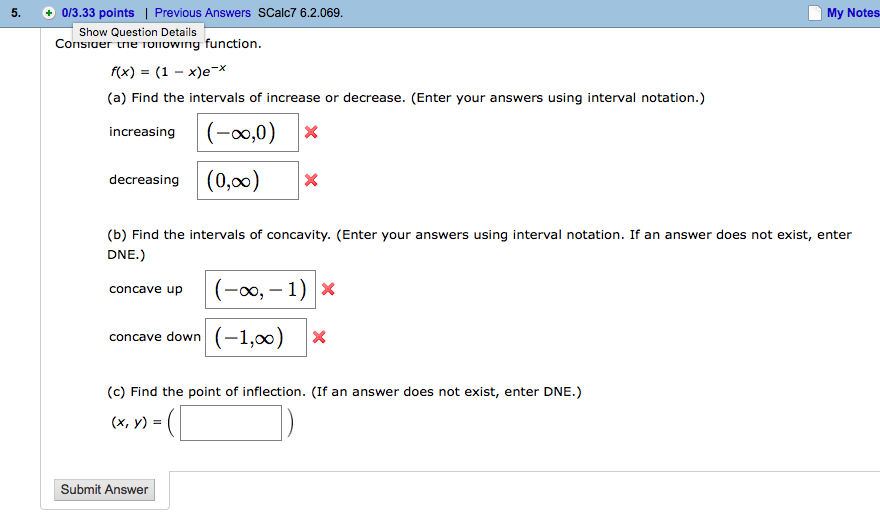



Consider The Following Function F X 1 X E X Chegg Com




Let F X E X 1 X 1 X N N Where N In N Show That F Is Non Increasing On 0 Infinity Study Com




Find The Intervals In Which F X Log 1 X X 1 X Is Increasing Or Decreasing Maths Application Of Derivatives Meritnation Com




Find The Intervals In Which The Function F X X 4 X 3 3 Is Increasing Or Decreasing



Www Hoodriver K12 Or Us Cms Lib Or Centricity Domain 230 Ch 5 pt answer key Pdf




Find The Intervals In Which The Function F Given By F X X 3 1 X 3 X 0 Is Mathematics Shaalaa Com



Http Euler Fd Cvut Cz Predmety Calculus1en Cal1 Soubory Files Exercises Monotony Pdf
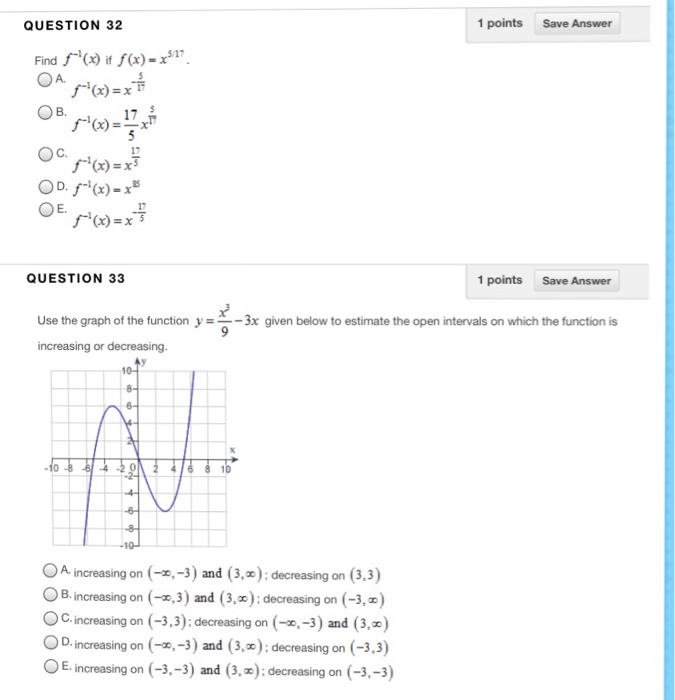



Find F 1 X If F X X 5 17 A F 1 X X Chegg Com




A Find The Intervals In Which The Function F X Log 1 X X 1 X Is I Increasing Ii Decreasing Function B Find The Intervals In Which The Function F X X Log E X X Gt 0 Is Increasing Or Decreasing



Find The Intervals In Which The Function F X X 1 3 X 2 2 Is Sarthaks Econnect Largest Online Education Community




F R Gt R F X X 1 X 2 Determine Intervals In Which The Given Function Are Strictly Increasing Or Brainly In



Pslv Soln Rational Functions



Q Tbn And9gcr1awjnfievvbxtiltp6vsfzl Yvhcce0yraat7t Hr3 P37lem Usqp Cau




Increasing And Decreasing Function 1 Strictly Increasing Function



Find The Intervals In Which The Function F X X 1 3 X 2 2 Is Sarthaks Econnect Largest Online Education Community



1




X Log X Increases In The Interval F X X Log X Increases In The Interval F X X Log X Decreases Youtube




1 Sinx In 9 1 In The Interval 1 0 X 5 2 7




Answered 1 For The Function F X X 1 E A Bartleby




Find The Intervals In Which F X X 1 3 X 2 2 Is Strictly Increasing And Strictly Decreasing Brainly In
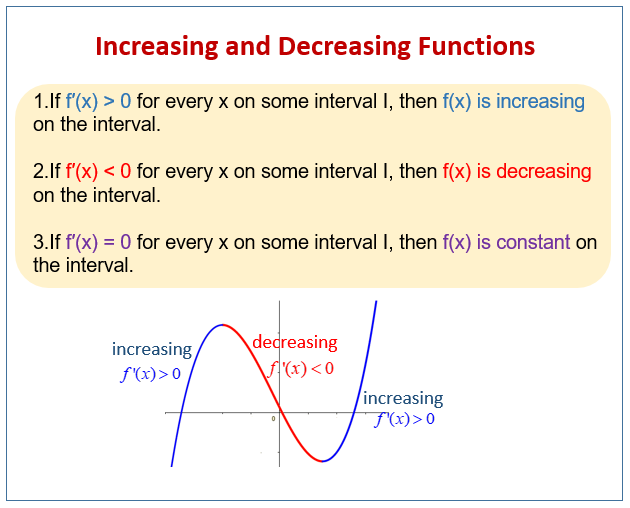



Increasing And Decreasing Functions Examples Solutions Worksheets Videos Activities




Increasing And Decreasing Function 1 Strictly Increasing Function




23 The Graph Of F X 1 2 1 X X 2 X 2 Is Chegg Com
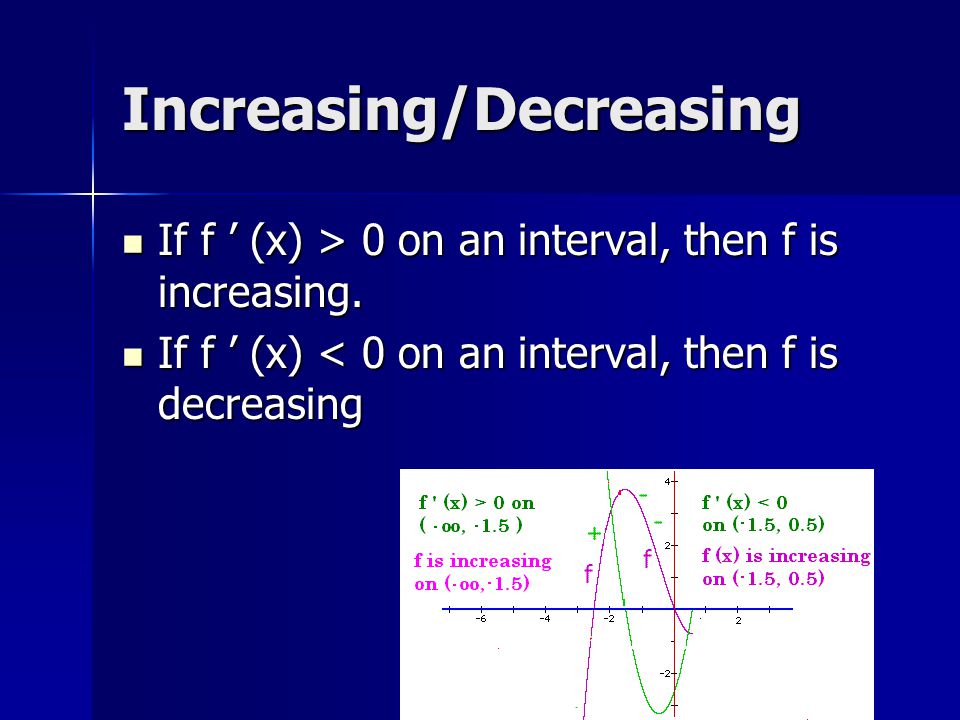



Increasing Decreasing Ppt Video Online Download



Increasing And Decreasing Functions




Ex 6 2 6 Find Intervals In Which Functions Strictly Increasing




Classxii Sub Mathematics Topic Increasing Decreasing Increasing Decreasing



Increasing Decreasing Functions Examples



Math Scene Functions 2 Lesson 2



Increasing And Decreasing Functions
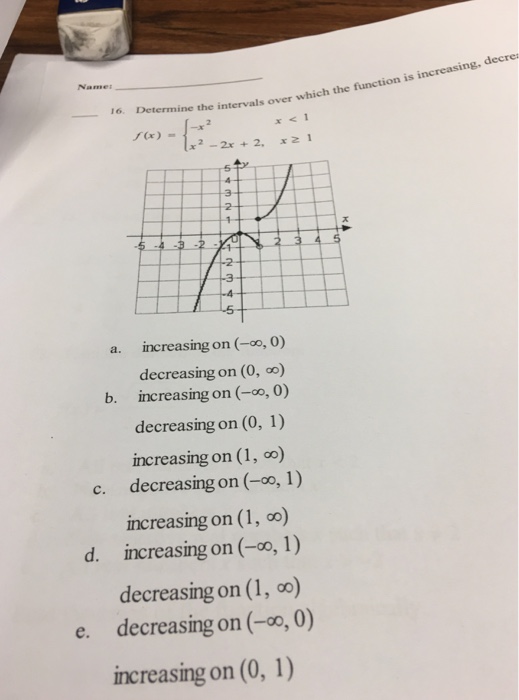



Determine The Intervals Over Which The Function Is Chegg Com



Day15




Rd Sharma Class 12 Solutions Chapter 17 Increasing And Decreasing Functions



Features Of Function Graphs Mathbitsnotebook A1 Ccss Math




The Function F X X 2 2x 5 Is Strictly Increasing In The Interval




Ex 6 2 11 Prove F X X2 X 1 Is Neither Strictly Increasing




Let I Be Any Interval Disjoint From 1 1 Prove That The Function F Given By F X X 1 X Is Strictly Increasing On I Mathematics Shaalaa Com




Solve This Q Find The Intervals In Which The Function F X 3 Log 1 X Maths Application Of Derivatives Meritnation Com
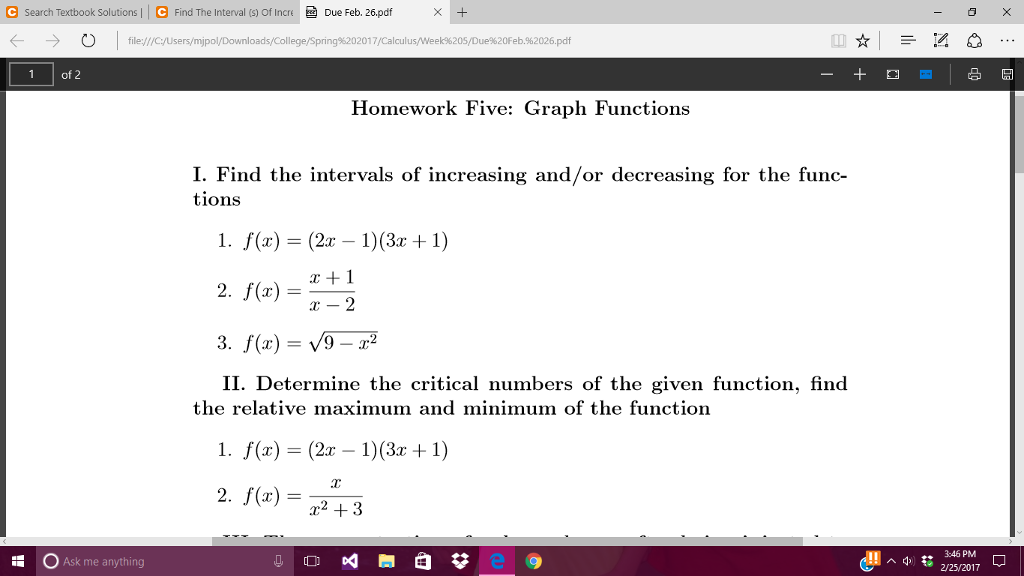



Find The Intervals Of Increasing And Or Decreasing Chegg Com




41 Increasing And Decreasing Functions Pdf Calculus Mathematical Objects
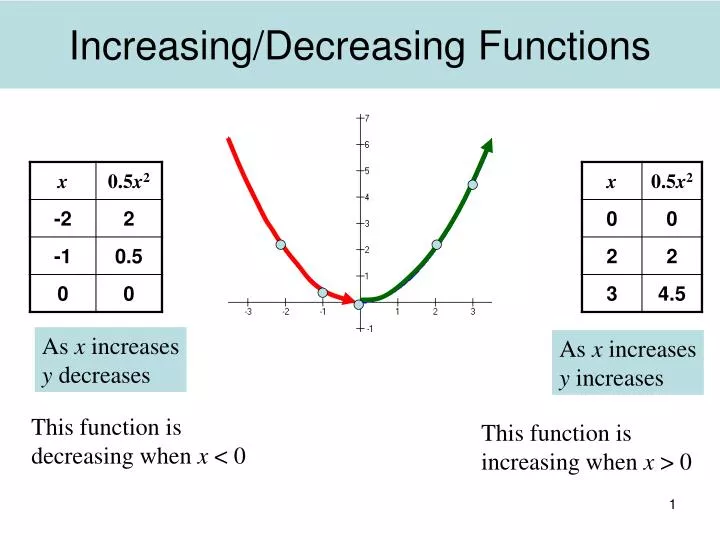



Ppt Increasing Decreasing Functions Powerpoint Presentation Free Download Id



Increasing And Decreasing Functions
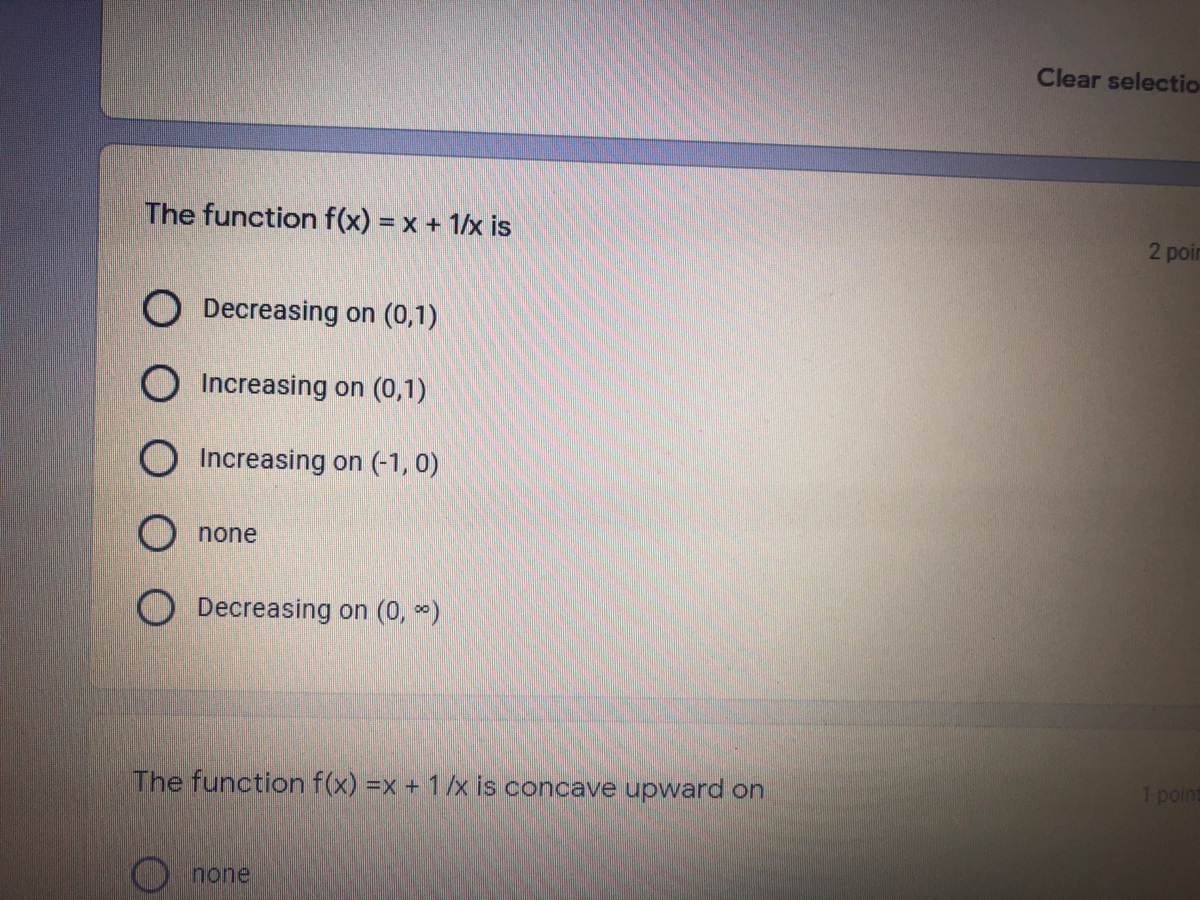



Answered The Function F X X 1 X Is 2p O Bartleby
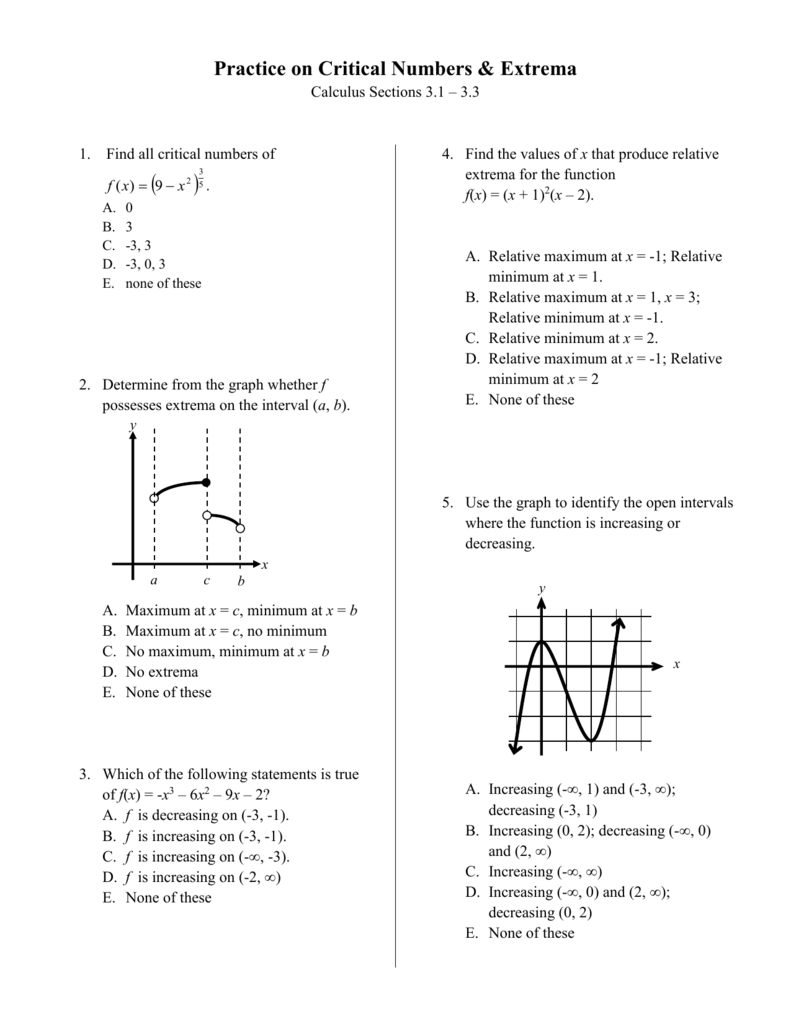



Practice On Critical Numbers Extrema



Find The Intervals Of Increase And Decrease For The Chegg Com



0 件のコメント:
コメントを投稿